Divisibility by 2
This is the easiest of divisibility rules and the very first one to use when checking divisibility of a number or if a number is prime.
A number is divisible by 2 if it ends in an even number. So, if the number ends in 0, 2, 4, 6, or 8, it’s divisible by 2.
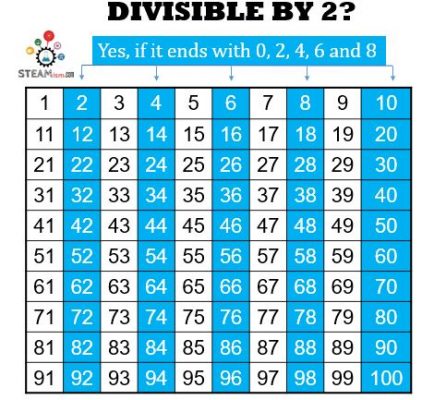
More Examples:
- 10222 – Yes, because it ends with a 2.
- 8,738,789 – Nope, ends with a 9.
- 783,897 – Again, no, ends with a 7.
- 93757374 – Yes! Ends with a 4.
Easy, right?
Divisibility by 3
This one’s surprisingly easy too!
Add up all the digits of the number. Is the sum divisible by 3? Then the entire number is divisible by 3!

More Examples:
- 98,71,654,323:
- Add up all digits: 9 + 8 + 7 + 1 + 6 + 5 + 4 + 3 + 2 + 3 = 48.
- Add digits again: 4 + 8 = 12.
- 12/3 = 4
- Yes, 98,71,654,323 is divisible by 3.
- 85,490
- Add up all digits: 8 + 5 + 4 + 9 + 0 = 26
- Add digits again: 2+6=8
- 8 is not divisible by 3.
- No, 85,490 is not divisible by 3.
Divisibility by 4
Remember divisibility by 2? This one is very similar! To be divisible by 4, the last 2 digits (units and tens place) of the number should be divisible by 4.
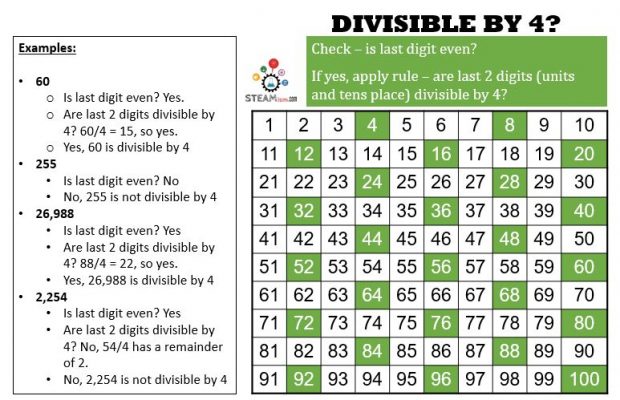
More Examples:
- 98,71,654,324:
- Last digit even? Yes.
- Last 2 digits divisible by 4? 24/4 = 6
- Yes, 98,71,654,324 is divisible by 4.
- Easy, huh?
- 85,492
- Last digit even? Yes.
- Last 2 digits divisible by 4? 92/4 = 23
- Yes, 85,492 is not divisible by 4.
Divisibility by 5
This one’s super-easy too, no pesky additions or divisions. Is the last (units) digit a 5 or a 0? Wham, it’s divisible by 5!
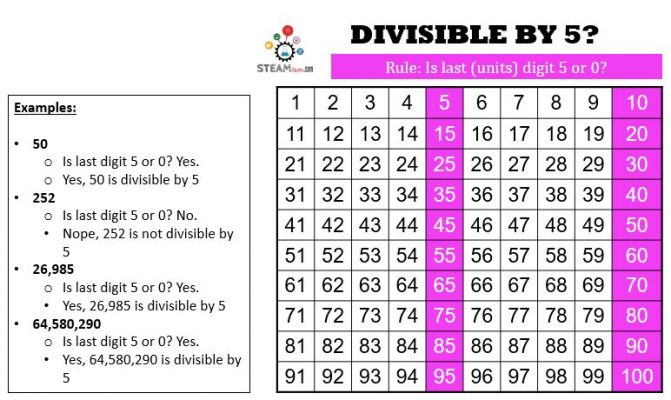
More Examples:
- 98,71,654,320:
- Last (units) digit 5 or 0? Yes.
- Yes, 98,71,654,320 is divisible by 5.
- 85,492
- Last (units) digit 5 or 0? No.
- No, 85,492 is not divisible by 5.
Divisibility by 6
While not as easy as some of the others, this one combines 2 easy rules – divisibility by 2 and 3. This makes sense if you think about the fact that 2 x 3 = 6.
- Check 1 – is it divisible by 2 ⇒ Are last (units) digit even (0, 2, 4, 6, 8)?
- If yes, Check 2 – is it divisible by 3 ⇒ Is sum of all digits divisible by 3?
More Examples:
- 98,71,654,3023:
- Last (units digit) even? No.
- No, 98,71,654,323 is not divisible by 6.
- 85,494
- Is last (units) digit even? Yes
- Add up all digits: 8 + 5 + 4 + 9 + 4 = 30
- 30/3 = 10.
- Yes, 85,494 is divisible by 3.
Divisibility by 7
This one’s actually fun with some practice, I promise! And makes you feel very smart for knowing such a cool trick!
- Multiply last (units) digit by 2.
- Now subtract from rest of the number.
- Rinse, repeat until number is small enough
- Is final number 0 or multiple of 7? Then the original number is divisible by 7
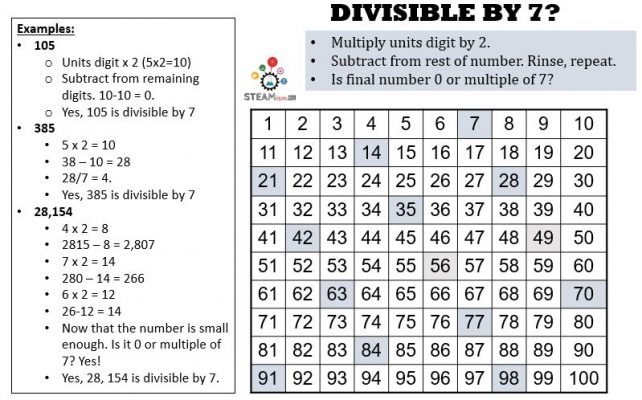
More Examples:
- 9,876,538 (this one is long and tedious and it may be easier to just divide by 7 but I wanted to show you a full method):
- Units digit x 2 (8 x 2 = 16)
- 987653 – 16 = 987637
- 7 x 2 = 14
- 98763 – 14 = 98749
- 9 x 2 = 18
- 9874 – 18 = 9856
- 6 x 2 = 12
- 985 – 12 = 973
- 3 x 2 = 6
- 97 – 6 = 91
- 1 x 2 = 2
- 9 -2 = 7
- Is this simplified number divisible by 7? Yes!
- Yes, 9,876,538 is divisible by 7.
- 31,696
- 6 x 2 = 12
- 3169 – 12 = 3157
- 7 x 2 = 14
- 315 – 14 = 301
- 1 x 2 = 2
- 30-2 = 28
- 28/7 = 4.
- Yes, 31,696 is divisible by 7.
Divisibility by 8
Remember the divisibility rule for 4? This one is almost the same. If the last three digits of a whole number are divisible by 8, then the entire number is divisible by 8.
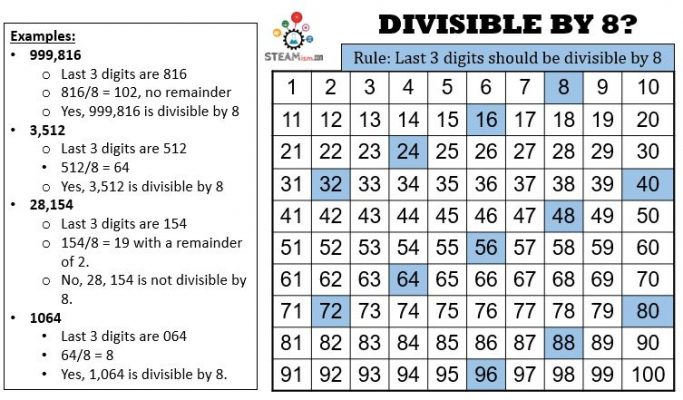
More Examples:
- 9,876,538:
- 538/8 = 67 with a remainder of 2.
- No, 9,876,538 is not divisible by 8.
- 31,696
- 696/8 = 87.
- Yes, 31,696 is divisible by 8.
Divisibility by 9
Remember the divisibility rule for 3? The same, with a small twist! Add up all the digits of the number. Is the sum divisible by 9? Then the entire number is divisible by 9!

More Examples:
- 98,71,654,320:
- Add up all digits: 9 + 8 + 7 + 1 + 6 + 5 + 4 + 3 + 2 + 0 = 45.
- 45/9 = 5.
- Yes, 98,71,654,320 is divisible by 9.
- 85,490
- Add up all digits: 8 + 5 + 4 + 9 + 0 = 26
- 26 is not divisible by 9.
- No, 85,490 is not divisible by 9.
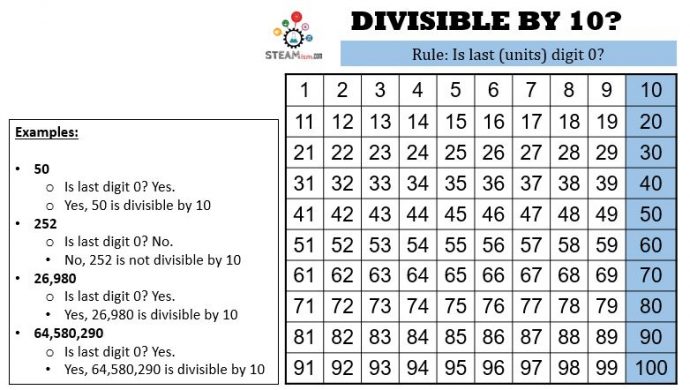
Divisibility by 10
This one is almost something that we learn in elementary school and doesn’t need to be explained. Does the number end with a 0? If yes, it’s divisible by 10. That’s it!
- How To Write A Lab Report - April 8, 2023
- The States (Phases) of Matter - June 9, 2020
- What is Engineering? - June 2, 2020
