To start with, what are odd and even numbers?
Right. Let’s start off with some definitions, then.
- What is an odd number? Any number that cannot be divided by 2.
- What is an even number? Any number that can be divided by 2.

What is a factor?
A factor is any number that can divide another number without a remainder.
So, for example,
- 4/2 = 2. No remainder.
- 9/3 = 3. No remainder.
- 11/1 = 1. No remainder. But, there’s a hint here…
What is a composite number?
A composite number is any number that can be divided by at least one other number (a factor) other than itself.
- In other words, composite numbers always have more than 2 factors (1, the number, any other factors).
- Examples? Oh, that’s easy.
- 4 = 2 x 2. So, 4 has 3 factors – 1, 2, and 2.
- 6 = 3 x 2. So, 6 has 3 factors – 1, 2, and 3.
Now, finally – what are prime numbers?
Prime numbers are the exact opposite of composite numbers.
- They are only divisible by the number 1 and themselves.
- In other words, a prime number can only have 2 factors.
So, 1 is a prime number then?
Aaahh, good question! No – 1 is a very special kind of number. It doesn’t even have 2 factors. It only has itself. So, nope – 1 is not a prime number.

So, which ones are the prime numbers then?
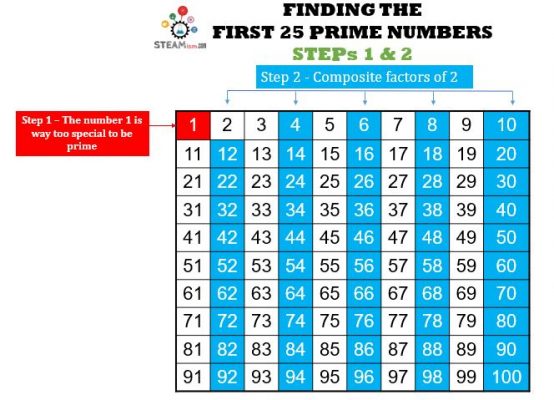
Let’s go through a quick exercise to find the first 25 prime numbers. Look below at the table with the first 100 numbers, 1 to 100.
Step 1 – We already know our friend, 1, is too special to be prime.

Step 2 – Composite factors of 2.
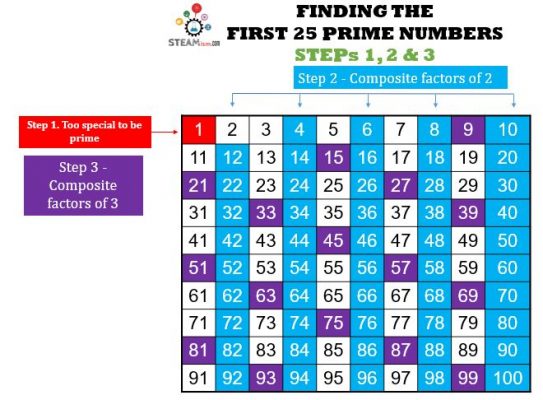
Step 3 – Composite factors of 3 (that are not already composite factors of 2).
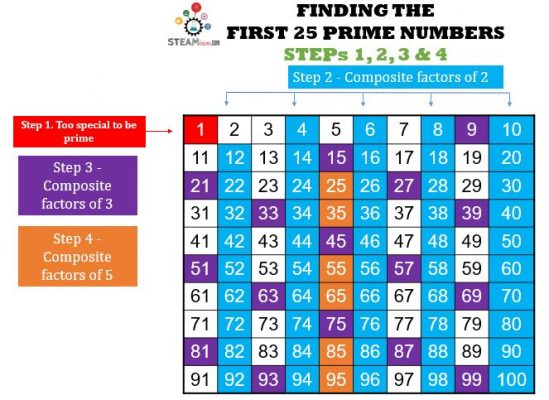
Step 4 – Composite factors of 5 (that are not already composite factors of 2 and 3).
Step 5 – Composite factors of 7 (that are not already composite factors of 2, 3 and 5).

Let’s blank out all the composite numbers and now we have the first 25 prime numbers!

Is that it? That’s not too bad – I could memorize this list pretty fast!
Uhhhhh, no, not really! Here’s a list of the first 50 million primes, in blocks of 1 million. More fun to memorize!
What’s the largest known prime today?
As of January 2018, the largest known prime number is 277,232,917 − 1, a number with 23,249,425 digits. It was found by the Great Internet Mersenne Prime Search (GIMPS). Here’s a wiki article on it.
And, in some “prime” news….
A Mathematical Breakthrough: Yitang Zhang and the Twin Prime Conjecture
- How To Write A Lab Report - April 8, 2023
- The States (Phases) of Matter - June 9, 2020
- What is Engineering? - June 2, 2020
