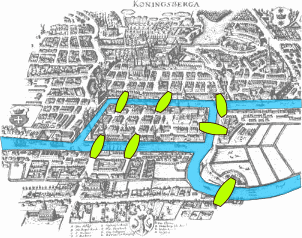
Königsberg is undoubtedly one of the most famous cities in mathematics, in part due to its interesting geography. The city of Königsberg (now Kaliningrad, in Russia) was built on two sides of a river, near the site of two large islands. The four sectors of the city were connected by seven bridges, as shown in the following map. Carl Ehler, a mathematician, was puzzled by a question — “Which route would allow someone to cross all 7 bridges, without crossing any of them more than once?”
Can you figure out such a route?
No, you can’t! In 1736, while proving that it’s impossible to find such a route, Leonhard Euler laid the foundations for graph theory.
Before we dive right in, let’s talk about certain preliminaries on graph theory we’ll need, to better understand this historical problem.

So, what is a graph? A graph is just a collection of nodes and edges (very different from the graphs you’ve seen in calculus!). For the sake of simplicity, throughout this post, we’ll talk only about undirected graphs — i.e. graphs wherein there is no sense of direction associated with the edges. Also, the number of edges touching a particular vertex correspond to its degree.

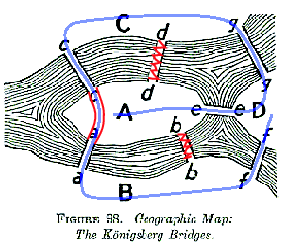
The map of the ancient city can be easily represented as the graph on the right (why?) — where the edges and nodes correspond to bridges and sectors of the city, respectively.
We’ve now developed sufficient weaponry to attack the problem, so let’s begin by formalizing what we’re looking for — an Euler walk. An Euler walk in an undirected graph is a walk (a sequence of alternating vertices and edges) that uses each edge exactly once. If such a walk exists, the graph is called traversable (which our graph is not!).
To get a bit more mathematical, let’s denote the start and end vertices with S and V respectively. Furthermore, consider the following minor yet critical observation — Every vertex that isn’t S or V, must have an even degree.
Why? Let’s give it some thought. The only way to pass a vertex that isn’t the start or the end vertex is by entering through an edge and exiting through another. Since we can’t use an edge more than once, this shows that the degree of all such vertices (not S or V) must be even. Note that there’s no restriction on how many times we visit a vertex, as long as we traverse all bridges (edges) exactly once.
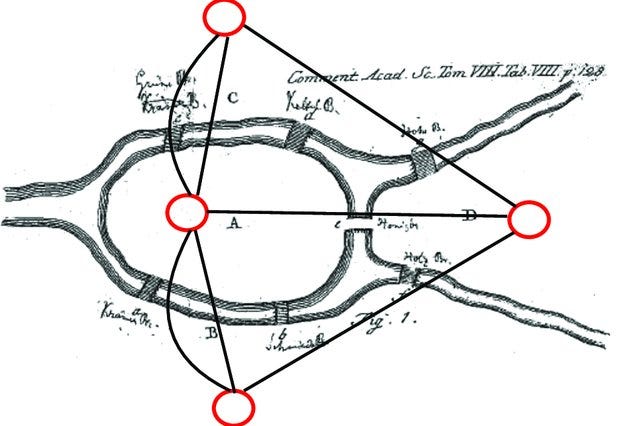
The map of Königsberg (as a graph) has at least three vertices with odd degrees, indicating that it is impossible to find a route with the desired properties! We solved it!
On a practical note, all the seven bridges were destroyed by a bombing raid in 1944 and only five of them were rebuilt. Königsberg became part of the Soviet Union (now Russia) at the end of World War II and was renamed Kaliningrad.
The bridges bb and dd were destroyed (and never rebuilt), and aa and cc are now a single bridge passing above A with a stairway in the middle leading down to A. Can you find an Euler walk in the map of modern-day Königsberg?
Read More:
1. Eulerian Walks
2. The Five Room Puzzle (A similar problem in Graph Theory)
3. The Seven Bridges of Königsberg (MAA)
4. On known and less known relations of Leonhard Euler with Poland (arXiv)
5. Modern-day Königsberg
- The Seven Bridges of Königsberg - August 17, 2020
- The Turing Test - August 6, 2020
- What is Machine Learning? - July 28, 2020