What is Plane Geometry?
Plane Geometry deals with flat 2-D (2 dimensional) shapes like lines, circles and triangles.
-
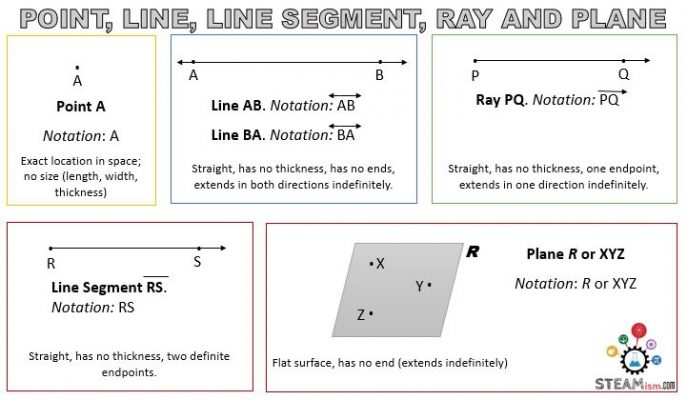
- Point: is the most basic element of all geometric figures. No dimension –> no length, no width, and no thickness. Describes the exact location or position on a surface or in space.
-
Line: is straight, has no thickness, has no ends –> extends in both directions indefinitely.
- Line segment: is straight, has no thickness, but ends at 2 distinct points.
- Ray: is straight, has no thickness, has one end point, and extends in one direction indefinitely.
- Plane: is a flat surface, has no end (extends indefinitely). Your wall or floor are examples of planes.
Point, Line and Plane Postulates and Theorem
A theorem is a true statement that can be proven. A postulate or an axiom is a statement that is accepted as true without any proof.
Points and Lines:
- The 2 Point Postulate: Through any two points there exists exactly one line.
- The Line-Point Postulate: A line contains at least two points.
- The Line Intersection Theorem: If two lines intersect, then they intersect in exactly one point.

Points and Planes:
- The 3 Point Postulate: Through any three non-collinear points, there exists exactly one plane.
- Plane-Point Postulate: A plane contains at least three non-collinear points.

Lines and Planes:
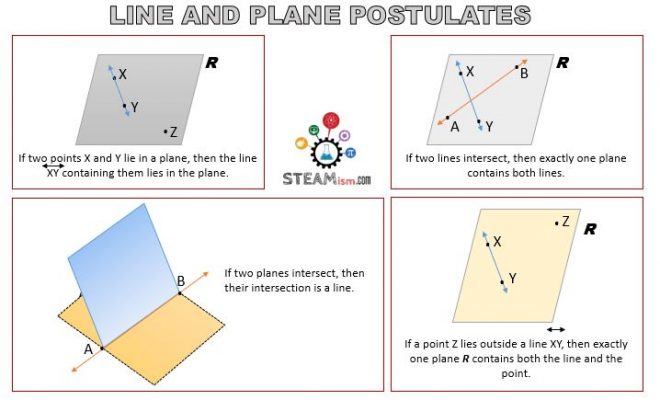
- Plane-Line Postulate: If two points lie in a plane, then the line containing them lies in the plane.
- Line Intersection Theorem: If two lines intersect, then exactly one plane contains both lines.
- Plane Intersection Postulate: If two planes intersect, then their intersection is a line.
- Point and Line contained in Plane Theorem: If a point lies outside a line, then exactly one plane contains both the line and the point.
Links
Need flash cards for quick review? Quizlet flashcards on points, lines and planes postulates and theorems
Latest posts by Aniruddha Pochimcherla (see all)
- An Interview with the Co-Founders of Dermanostix - August 14, 2020
- NASA & SpaceX’s Successful Space Launch - June 12, 2020
- Types of Engineering - June 10, 2020
